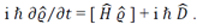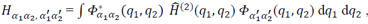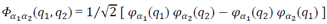In this book, the author opens up new possibilities for the main quantities in
quantum physics – the statistical operator 𝜚̂ and the density matrix_𝜚𝑛𝑚. The
meaning of the density matrix is that its diagonal elements 𝜚𝑛𝑛 are equal to the
probability 𝑤𝑛 that the system in the quantum state n. The point in this book is
the Lindblad equation for the statistical operator 𝜚̂, where the main element of
influence on the system of its environment is the dissipative operator 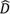 :
:
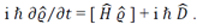
This operator is written in the most General form. In order for the Lindblad
equation to be solved, the 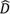 operator must be specified. The author wrote down
the dissipative diffusion and attenuation operators that will allow us to find the
operator must be specified. The author wrote down
the dissipative diffusion and attenuation operators that will allow us to find the 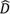 operator. Now, this operator depends on the temperature T and describes the
effect of the thermostat R on the quantum system S. This new equation is not
difficult to write for the particle density matrix in coordinate representation as
compared to the Wigner equation, which coincides with the Fokker – Planck
equation. This proved the equivalence of quantum physics and classical statistical
physics.
operator. Now, this operator depends on the temperature T and describes the
effect of the thermostat R on the quantum system S. This new equation is not
difficult to write for the particle density matrix in coordinate representation as
compared to the Wigner equation, which coincides with the Fokker – Planck
equation. This proved the equivalence of quantum physics and classical statistical
physics.
The author wrote the Lindblad equation for a harmonic oscillator and inserted a
dissipative attenuation operator into it. And without any approximation, he
derived the equation of damped oscillations for the average value of the 𝑥̅(t)
coordinate with absolute accuracy.
Bondarev based on the Lindblad equation with another operator 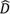 developed the
theory of the harmonic oscillator, in which he found the density matrix and
proved the Heisenberg relation.
developed the
theory of the harmonic oscillator, in which he found the density matrix and
proved the Heisenberg relation.
He further developed the theories of the light diode and ball lightning. In light
diode theory, he used the diffusion and attenuation operators and derived the
Fokker – Planck equations for electrons and holes. These equations present the
terms that are responsible for radiation.
The theory of ball lightning is based on the assumption that the gas inside the ball
is completely ionized and electrons, due to their lightness in comparison with
nuclei, evenly fill this ball. The equation for the statistical operator 𝜚̂ nuclei
contains operators of diffusion and damping. This equation is a second-degree
equation with respect to the coordinate and momentum operators. The probability
of distribution of nuclei over the volume of a ball lightning is found.
Bondarev derived von Neumann equation from the Liouville, which is valid for a
non-equilibrium system S and an equilibrium thermostat R, the equations for the
density matrix S of a single particle and a system of identical particles. These
equations have a remarkable property. When the density matrix has a diagonal
form, they get turned into quantum kinetic equations for probabilities, which are
obtained in the wave graphical representation.
The book presents new theories of such experimentally discovered phenomena as
step kinetics of bimolecular reactions in solids, superconductivity, superfluidity,
energy spectrum of an arbitrary atom, laser, spaser and graphene.
Kinetics is called as a stepwise process, in which the reaction suddenly stops at a
constant temperature even in the presence of a lot of reagents. But as soon as the
temperature is raised, the reaction starts again. The reason for this reaction is the
tunnel effect, which is observed only in solids, when there are molecules in the
bodies that hold the reagents near them. In liquids, these molecules can move
along with the reagents and enter into a reaction that goes all the way while there
are reagents. The reaction in liquids always obeys the Arrhenius law. To describe
stepwise kinetics, the author came up with a correlation theory.
So, when processing the results of the step kinetics experiment using correlation
theory, it was found that the Arrhenius law is also fulfilled here. And there was
also an increase in localization volume with increasing temperature, as predicted
by the tunnel effect.
Superconductivity can be described by the law of changing the probability 𝑤𝒌 of
filling the state of electrons with the wave vector k as a function of temperature.
This law has long been known. It depends on the energy 𝜀𝒌𝒌′ of the interaction of
electrons with the wave vectors k and 𝒌′. When 𝜀𝒌𝒌′ = 0, the probability 𝑤𝒌
obeys the Fermi − Dirac law. Our goal was to find the energy 𝜀𝒌𝒌′ of the
interaction of electrons.
We denote the matrix elements of the interaction Hamiltonian of two particles as
𝐻12,1′2′ , where 1 is the spin quantum number of the particles. If the particles are
bosons, then the matrix elements must be antisymmetric, i.e. then the matrix
elements must change the sign when replacing variables 1 and 2, or 1′ and 2′.
This is possible if the matrix elements represent the sum of two terms of different
characters. In the wave representation, the energy ε_(kk^') will also represent two
terms of different signs. But in this case, it is very difficult to solve the equation.
Therefore, we roughly denote these terms as
𝜀𝒌𝒌′ = I 𝛿𝒌 + 𝒌′ − J 𝛿𝒌 − 𝒌′ ,
where I and J are positive constants, 𝛿𝒌 is the Kronecker symbol. Now we can
substitute this function into the equation and get
ln [ ( 1 − 𝑤𝒌 ) ⁄ 𝑤𝒌 ] = 𝛽 ( 𝜀𝒌 + 𝐼 𝑤− 𝒌 − 𝐽 𝑤𝒌 − 𝜇 ) .
This equation has a remarkable property. For some areas of 𝒌 will this inequality
be true
𝑤𝒌 ≠ 𝑤− 𝒌 .
The property that is expressed by this inequality is called anisotropy. The
appearance of this property here is superconductivity.
Solving this equation, we obtain for T = 0 functions that have five values for one
argument value. Since this function describes stationary states, the lowest energy
is the value of the function where the electrons remain indefinite. This will be a
superconducting state.
In theory, the parameter represents f = ( 𝐽 − 𝐼 ) ⁄ ( 𝐽 + 𝐼 ). This parameter divides
superconductivity into two kinds. If 0 ≤ f ≤ 1, then it is a I-type superconductor,
and if −1 ≤ f < 0, then it is a II-type superconductor. Critical temperature is
defined as 𝑇𝑐 = ( 𝐼 + 𝐽 ) ⁄ ( 4 𝑘B). All the main effects and properties of superconductors are covered by this theory.
In the theory of superfluidity for liquid helium, Не3 and Не4, all values that
express the properties of this mixture are described by functions having multiple
values in a certain temperature range. As a consequence, the heat capacity tends to
infinity when the temperature approaches the temperature 𝑇𝜆 of the lambda
transition.
The theory of the energy spectrum of an arbitrary atom begins with determining
the energy using statistical operators:
E = ∫𝐻(1) 𝜚̂(1) dq + 1 2 ⁄ ∫𝐻(2) 𝜚̂(2) d𝑞1 d𝑞2 ,
where 𝐻 ̂ (1) is the Hamiltonian of one electron, 𝐻 ̂(2) is the Hamiltonian of two
interacting electrons, 𝜚̂(1) and 𝜚̂(2) are the statistical operators of one and two
electrons. The matrix 𝐻𝛼1𝛼2, 𝛼1
′ 𝛼2
′ of the Hamiltonian 𝐻 ̂ (2) must be antisymmetric.
To do this, it is taken equal to
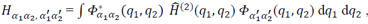
where
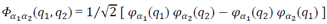
there is an antisymmetric Slater function. The eigenfunctions of electrons in the
hydrogen atom are taken as functions 𝜑𝛼(𝑞). After a series of calculations, an
equation is obtained from which one can obtain the eigenfunction and energy
𝜀𝑛 𝑚 𝑙 𝜎 of electrons of an arbitrary atom.
In the following chapters, new theories of the laser and spaser are constructed,
which are similar to each other in the content of the main quantum approaches to
describing the phenomena occurring in them. The basis of these theories is the
Lindblad equation. The equation for the density matrix will be written in a
coordinate form with a known Hamiltonian and an unknown dissipative matrix.
To find this matrix, we need to remember that we know the kinetic equation for
active atoms, which follows from the equation for the density matrix in the
representation where it has a diagonal form. So, a representation needs to be find
out where the density matrix has a diagonal form. The closest to this
representation is the representation in which the Hamiltonian of active atoms will
also have a diagonal form. Thus, the Hamiltonian has two representations. One α-
representation is a coordinate representation. The other is the 𝜅-representation, in
which the Hamiltonian has a diagonal form. These two Hamiltonians are
connected by the unitary matrix 𝑈𝛼𝜅. The density matrices 𝜚𝛼𝛼′ and 𝜚̃𝜅𝜅′ will also
be connected by the same unitary transformation:
𝜚𝛼𝛼′ = Σ𝜅𝜅′ 𝑈𝛼𝜅 𝜚̃𝜅𝜅′𝑈∗𝛼′𝜅′ .
We find the dissipative matrix in the 𝜅-representation.
Now we need to create another equation in the α-representation. This is the most
important equation in laser theory. This is the equation for the spectral energy
density of radiation. To solve it, we will use the density matrix 𝜚𝛼𝛼′ . As a result,
we will have the spectral energy density of the radiation from the laser.
Almost free electrons wander along the surface of graphene. For every carbon
atom, there is one such electron. To obtain the kinetic equation of these electrons,
their Hamiltonian must be reduced to a diagonal form. After these
transformations, we will have a system of two equations that are equivalent to the
equation obtained in the theory of superconductivity.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors confirm that there is no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.
Boris V. Bondarev
Moscow Aviation Institute (National Research University)
Moscow
Russia


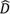 :
: